Умножение ЧПЗ
Требуется вычислить

Z=X*Y=qxSPx*qySPy= qxqyS(Px+Py)=qzSPz .
Алгоритм выполнения операции состоит в следующем:
- мантиссы сомножителей перемножаются;
- порядки сомножителей складываются;
- произведение нормализуется;
- произведению присваивается знак в соответствии с алгоритмом, приведенным для ЧФЗ, а именно:
- алгебраическое суммирование порядков – это операции над целыми числами или ЧФЗ с фиксацией точки справа от МЗР;
- перемножение мантисс – это операции над правильными дробями или над ЧФЗ с фиксацией точки слева от СЗР;
- определение знака произведения.
- если мантисса X или Y равна 0, то перемножение не проводится и Z=0;
- если при суммировании PX и PY возникло переполнение и PZ<0, то это означает, что Z меньше минимального представляемого в машине числа, и Z присваивают 0 без перемножения мантисс;
- если при суммировании PX и PY возникло переполнение и PZ>0, может оказаться, что Z все же находится в диапазоне представляемых в ЭВМ чисел, так как после нормализации полученного qZ
переполнение в порядке может исчезнуть.

В данном случае имеется в виду способ умножения, предполагающий отделение от сомножителей их знаковых разрядов и раздельное выполнение действий над знаками и модулями чисел. Однако на практике в современных ЭВМ используют алгоритмы, не требующие раздельных операций над знаками и модулями, например алгоритм Бута. Информацию о них можно найти в литературе, приведенной в конце главы.
Рассмотрим простейший раздельный алгоритм перемножения ЧПЗ.
Умножение ЧПЗ сводится к следующим операциям:
Операции над целыми числами были рассмотрены ранее. Теперь рассмотрим только перемножение правильных дробей. Вручную дроби можно перемножать столбиком. Подсчет знаков в дробной части такой же, как и при перемножении десятичных дробей. В ЭВМ для перемножения мантисс (как и для целых чисел) возможны два варианта перемножения: "старшими разрядами вперед" и "младшими разрядами вперед".
Если требуется сохранить все разряды, то в устройстве, формирующем произведение, число разрядов должно равняться сумме числа разрядов множителя и множимого. Однако часто в произведении требуется сохранить то же количество разрядов, что и в множимом. Это приводит к потере младших разрядов.
Рассмотрим пример перемножения двух чисел "младшими разрядами вперед" для случая, когда разрядная сетка результата соответствует разрядной сетке сомножителей.
Пример.
Вычислить Z=X*Y=0.1101(2)
* 0.1011(2) = 0.8125(10) * 0.6875(10) = 0.55859375(10).
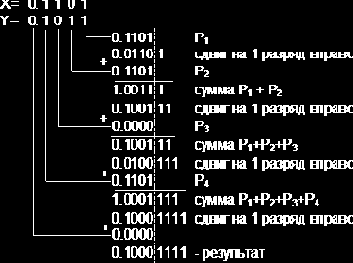
Таким образом, результат Z=0.1000(2)=0.5(10), поскольку последние четыре разряда потеряны.
При перемножении мантисс ( правильных дробей) последнее сложение можно не делать, а ограничиться просто последним сдвигом. Из примера видно, что если разрядная сетка ограничена числом разрядов X, то результаты правее вертикального пунктира не фиксируются после выполнения сдвигов. Таким образом, четыре младших разряда будут потеряны, и результат будет приближенный 0.1000(2). В ряде случаев используется округление по правилу: если старший из отбрасываемых разрядов содержит 1, то к младшему из сохранившихся разрядов добавляется 1. В данном примере получается число 0.1001(2).
В заключение отметим следующее: